Ecuación General de los Gases Ideales
🔍📚Química General: PxV=nxRxT🔍📚
Para continuar con las Leyes de los Gases y poder aplicar los conceptos que vimos del comportamiento de las variables involucradas (volumen, presión, temperatura, masa), vamos a analizar en detalle la Ecuación General de los Gases Ideales:
Cuando analizamos el comportamiento de los gases vimos que había una relación entre P, V y T; siempre y cuando se mantuviese constante la masa del gas estudiado.
Volumen molar y Constante (R) de los gases ideales
Se sabe que 1 mol de moléculas de cualquier gas ocupa el mismo volumen molar = 22,4 dm3. mol-1 (Donde dm3= decímetro cúbico). Por lo tanto, si consideramos una masa de gas igual a su masa molar, la expresión:
Veamos los siguientes ejemplos:
a) 32 g de O2 a 273 K y 1 atm de presión ocupan 22,4 dm3
Entonces podemos afirmar que para 1 mol de moléculas de O2:
b) 2g de H2 a 273 K y 2 atm de presión ocupan 11,2 dm3 ,esto se debe a que tengo el doble de masa (2 moles) que ocupa la mitad del volumen porque está al doble de presión, si realizamos la misma cuenta:
Fórmula general para calcular la constante molar de los Gases Ideales
En forma general podemos considerar que para 1 mol de moléculas de cualquier gas es igual a:
El valor de R no depende de la naturaleza del gas, es universal. La constante R suele llamarse: Constante Molar del Gas Ideal.
En el S.I. el valor de R resulata ser: 8,314 J x K-1 x mol-1
Como VM = V/n podemos expresar matemáticamente la dependencia de 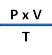con n (número de moles) con la siguiente escuación:
Como puede observarse todas las variables están relacionadas y resumidas en una sola expresión matemática. Se puede ver en esta ecuación que la presión es inversamente proporcional al volumen (PxV) y que es directamente proporcional a la temperatura y a la masa ( T y n).
Aplicaciones de esta ecuación
Ejemplo 1:
¿Qué volumen ocupan 3,0 moles de moléculas de O2 a 27°C y 2,0 atm?
Para poder aplicar la fórmula, primero tenemos que ver que las unidades de los datos sean las que necesitamos para que el cálculo sea compatible con R (atm x dm3 / K x mol).
Tenemos la masa en moles, OK 👌, la presión está en atm, eso también está bien 👌, y la temperatura está en °C, asi que la pasamos a K así: 27 + 273 = 300K.
Ahora estamos en condiciones de aplicar la ecuación del gas ideal:
Queremos averiguar el volumen, así que despejando obtenemos:
V= (nxRxT)/P
Ejemplo 2:
En un balón de 5,0 dm3 con tapa se mezclan 32 g de O2 con 2,8 g de N2 a 0°C. ¿Cuál es la presión del sistema?¿Cual es la presión parcial de cada gas?
Sabemos que 1 mol de O2 equivale a 32 g (podes verlo en una tabla periódica). De la misma forma podemos saber que 1 mol de N2 equivale a 28 g.
Estamos en condiciones de conocer entonces cuantos moles de cada gas están contenidos en el balón:
nO2= 32 g/ 32g x mol-1= 1 mol de O2
nN2= 2,8 g/ 28 g x mol-1= 0,10 moles de N2.
Para calcular la presión del sistema, debemos considerar la suma de los moles: 1 + 0,1= 1,1 moles. Esto es la Presión Total (Pt):
Entonces para responder ¿Cuál es la presión del sistema?
Y para responder esta pregunta ¿Cual es la presión parcial de cada gas?
Para el gas oxígeno:
Para el gas nitrógeno:
De esta forma calculamos las presiones parciales, es decir la presión que ejerce cada gas individualmente y la presión total del sistema.
Referencias
Soy Licenciada en Ciencias Biológicas y tengo un PhD en Química Biológica. Escribo esta página basada en mi experiencia como docente e investigadora y utilizo fuentes de información confiables para la redacción de los artículos:
