Leyes de los Gases

📐📚Leyes de los Gases. Gases Ideales.📏📚

En esta ocasión me gustaría explicar un tema que interesa a muchos estudiantes de Química General e Inorgánica y que suele ser un buen ejemplo del tratamiento de muchas variables dentro de un mismo sistema.

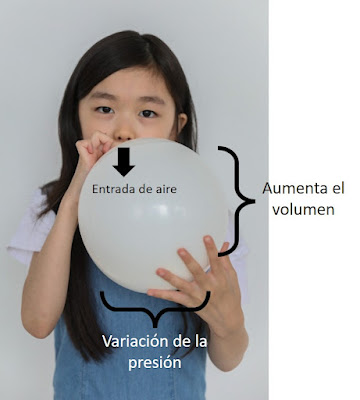
Pensemos en el siguiente ejemplo, ¿qué pasa cuando inflamos un globo?

El aire que introducimos, provoca que el globo se infle y su superficie se estire hasta un cierto límite, que será, cuando el globo estalle.

¿Qué le sucedió al sistema?

Se introdujo aire y el sistema respondió a esa perturbación variando su Masa, Presión y Volumen. Esto significa que estamos contemplando al menos 3 variables que están de alguna manera relacionadas y determinan el estado del sistema.

Variables del sistema

Ahora pensemos en un neumático de un auto que recorre por ejemplo, 100 km. Si se mide la presión de dicho neumático antes y después de haber recorrido cierta distancia, vamos a notar que la masa no ha variado, no se perdió masa del neumático, pero sí notaremos que la presión varió. Esto es el resultado de otra variable más, la Temperatura (Figura 1).

Figura 1. Un neumático de un vehículo es el ejemplo ideal de las variables de un sistema gaseoso.

En resumen, hay muchas variables en juego:

1. Masa
2. Presión
3. Volumen
4. Temperatura

Todas estas variables generan una perturbación en el sistema. Para entenderlas, se han desarrollado leyes surgidas de la experiencia que nos permiten comprender la relación entre presión y volumen a temperatura constante o la relación entre volumen y temperatura a presión constante. 

Cabe aclarar que es necesario dejar una variable constante para poder simplificar el sistema. De no contar con una constante, sería muy complicado entender qué parámetro afecta a otro si todo está variando al mismo tiempo.

Veamos entonces el resultado de las experiencias realizadas, que dieron lugar al establecimiento de las Leyes de los Gases:

Ley de Boyle-Mariotte

La relación matemática que existe entre la presión y el volumen a una masa fija de gas y a temperatura constante, fue descubierta por Robert Boyle en 1662.

 La siguiente tabla muestra como varía la presión en función del volumen de una masa constante de gas (10 g) a una temperatura constante (25°C):

Figura 2. Ley de Boyle-Mariotte

De este análisis de datos podemos deducir que para una masa fija de gas a una temperatura constante obtenemos una gráfica que corresponde a una hipérbola, por lo tanto, P x V = constante. Es decir que el volumen ocupado por una determinada masa de gas a una dada temperatura, es inversamente proporcional a la presión y lo mismo al revés. La presión ejercida por una masa de gas es inversamente proporcional a su volumen.

Figura 3. Si la presión aumenta, el volumen disminuye y si la presión disminuye, el volumen aumenta. Se trata de una relación inversamente proporcional.

La fórmula sería:

Donde k (m,T) es la constante de proporcionalidad a una masa de gas constante y temperatura constante.

Como podemos ver en el gráfico, el volumen aumenta linealmente con la temperatura. Si hiciéramos este experimento con cualquier gas, y ponemos como valor de volumen 0°C, obtenemos siempre el valor de T=-273,15 °C; es decir…¡¡la temperatura más baja posible!!

Convirtiendo entonces todos los valores usados en la tabla del gráfico a K y volviendo a graficar, obtenemos:

Figura 6. Relación lineal entre el Volumen (dm3) y la Temperatura en Kelvin (K).

Finalmente vemos que existe una relación de proporcionalidad directa entre el volumen y la temperatura en la escala Kelvin. Esto facilita mucho los cálculos en los que estas magnitudes están involucradas. Por lo tanto, a modo de conclusión, la relación entre la temperatura y el volumen de una masa de gas constante es la siguiente:

Esta relación implica que el volumen de un gas disminuye al disminuir T y debería anularse a T =0. Esto, por lo tanto, sugiere que el 0 en la escala de Kelvin es la menor temperatura posible. 

Una temperatura inferior implicaría un volumen negativo y eso no tiene  sentido físico. Recordemos que por más que matemáticamente se pueda calcular una variable, estamos  sujetos a las leyes físicas.

Figura 8. Cuando la temperatura aumenta, el volumen del sistema aumenta. Cuando la temperatura baja, el volumen del sistema disminuye.

Por último, si se obtienen experimentalmente valores de Presión y se grafican en función de la temperatura absoluta (a masa y volumen constantes) obtenemos que la presión es directamente proporcional a la temperatura. Gráficamente:

Figura 9. La presión es directamente proporcional a la temperatura.

Al combinar estas observaciones en una sola ecuación (ver el artículo Ecuación General de los Gases Ideales) que resuma el comportamiento de los gases, obtenemos:

Figura 11. Expresión matemática general de los gases

Donde podemos ver la relación inversamente proporcional entre la presión y el volumen y la relación directamente proporcional entre la presión y la temperatura así como entre la temperatura y el volumen. 

Aquí vemos también que la n representa la masa del gas, que se expresa en moles y R que es la constante universal de los gases ideales que siempre es este valor: 0,082 (atm x L / K x mol).

Referencias

Soy Licenciada en Ciencias Biológicas y tengo un PhD en Química Biológica. Escribo esta página basada en mi experiencia como docente e investigadora y utilizo fuentes de información confiables para la redacción de los artículos:

1. Temas de Química General. M. Angelini. Ed Eudeba, 2007  

Hasta aquí el contenido de hoy. Espero que te sirva y puedas usarlo para estudiar.

¡¡No olvides comentar y consultar lo que no entiendas!!